Gift exchange
MP 68: A bit of practical work, and a bit of fun.
My extended family, like many families I imagine, has people with all kinds of religious beliefs. One thing we all share, despite our vastly different beliefs, is the joy in giving gifts around this time of year.
We try to do a gift exchange most years. In past years someone would take pieces of paper, write everyone’s names on them, and pull them from a hat to see who each person would be paired up with. This lets everyone be more thoughtful about what they give. This year someone asked if I could write a program to match people up, without having anyone matched with a member of their immediate family.
This is the kind of task that’s often not worth automating, because you can easily spend more time writing the program than you actually save. But I had time one morning last week, and there’s a fun joke waiting on the other side of this work, so I said I’d be happy to give it a try.
First pass
This is the kind of program that’s been written thousands of times, so you could probably look it up and find a program someone else wrote and just run it against your own family’s names. But it’s also the kind of specific task that’s fun to play with without looking at other people’s work. I wanted to come up with something that works, share the results with our family, and then consider what more efficient solutions might look like.
First, we need a list of all the names of people participating in the gift exchange:
names = [
"Sherri",
"Eric",
"Terri",
"Joel",
"Joshua",
"Catherine",
"Jasmine",
"Alexandra",
"Jeremiah",
]I used Faker to generate this list of names, but inserted my own name into the list for a reason you’ll see in a moment.1
Matching constraints
It might actually be worth writing a program to deal with a small matching problem like this, because matching people while meeting a set of constraints can be hard to do manually. The only constraint in our gift exchange is that partners shouldn’t be assigned to give gifts to each other.
Here are the partners in my (fake) family:
partners = [
("Sherri", "Eric"),
("Terri", "Joel"),
("Joshua", "Catherine"),
("Jasmine", "Alexandra"),
]The constraint is implemented as a list of tuples. If any match we make includes one of these pairs, we need to reject that match.
Failed attempts
I always like to be honest about the background work I did before a writeup like this, because it’s easy to give the impression that I came up with a working solution on my first attempt. That’s rarely the case in my work, and the same is true for most of the programmers I know.
In my very first attempt I had it in my head that I needed to make pairs of people. I thought we needed to have an even number of participants for this to work. When I was looking at the first set of results I realized only half the people were giving gifts, and half were receiving gifts. That was a little facepalm moment, but it’s also something I love about programming. You can take an idea you have for a small problem, and try implementing it without having to think it through too deeply. The immediate feedback you get from trying something is invaluable, and almost always leads to a better understanding of the problem you’re trying to solve.
In my second attempt, I wrote a big nested loop. The outer loop kept running until a good set of matches was found, and the inner loop ran as long as there were still names that needed to be matched. That approach could work, but I find it hard to reason about nested while loops. I got a working solution by moving the body of the loops into functions, which greatly simplified my reasoning about the code.
Verifying matches
My main approach is to identify a list of givers and receivers. I should end up with nine sentences like this:
Eric will give to Alexandra.This pairing would work, because it doesn’t violate the constraints defined in partners.
We need a function to check whether a match works or not:
def check_match(match):
if match in partners:
return False
if tuple(reversed(match)) in partners:
return False
return TrueEven though we’re going to output sentences, the actual matches are going to be tuples like this:
('Catherine', 'Joshua')In check_match(), we want to make sure the current match is not in the list partners. If it is, we return False. If the match is not in partners, we also need to check whether the reversed version of the tuple is in partners. We only return True if both of these checks pass.2
When writing a function like this, it’s good to make a quick check that it works as expected:
print(check_match(('Sherri', 'Eric')))
print(check_match(('Eric', 'Sherri')))
print(check_match(('Sherri', 'Terri')))The first two should fail because these matches are in the list partners. The third match should work.
False
False
TrueThe function seems to work, so we can move on. (If this were part of a longer-term project, I’d move this code to a test.)
Matching everyone
Now we need a function that takes the list of names, and tries to match everyone. I’m sure there are a number of ways of solving the problem of matching people for the purpose of giving gifts, and I’m sure some approaches are better than others. But I’m matching nine people for a family event, so I’m not too worried about finding the best solution, or a mathematically elegant solution. A lot of times in programming, you don’t need to find the best solution. You just need to find something that works, and you can then refine your solution as needed.
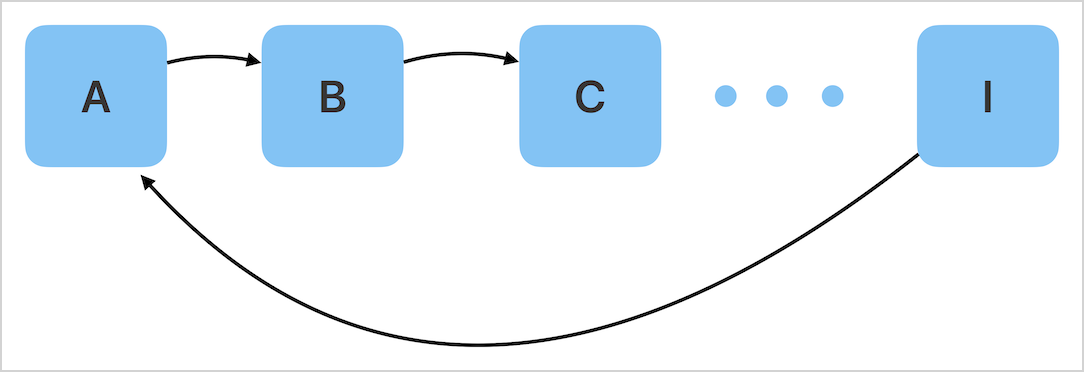
I’m going to try the following approach:
Shuffle the list of names.
Have person A give to person B, person B give to person C, and so forth.
That should take care of everyone except the first person and the last person. The first person has only given a gift, and the last has only received a gift. So, the last person will give a gift to the first person.
If this results in a match that doesn’t work, we’ll start over with a new shuffling of the original list.
Attempting a set of matches
Now we can write a function that attempts to make a full set of matches. The function will be given a copy of the original list of names, so it’s free to modify its copy of names:
def attempt_match(names):
random.shuffle(names)
matches = []
# Keep track of first giver.
giver = names.pop()
first_giver = giver
while names:
# Receiver is next name in list.
receiver = names.pop()
match = (giver, receiver)
# Bail if it's a bad match.
if not check_match(match):
return False
# Store match.
matches.append(match)
# Current receiver becomes next giver.
giver = receiver
# The last receiver gives to the first giver.
match = (receiver, first_giver)
if not check_match(match):
return False
# If we're still here, all matches are good.
return matchesThe comments in here should help make sense of this code. We first shuffle the names, so everyone is in a random order. We then make an empty list to store matches in.
We need to keep track of the first person assigned to give a gift, because they’ll need to be matched with the last person in the list when we’re all done.3 So before starting the loop, we call pop() to pull a name from the list. This is the first person assigned to giver, but we also assign that name to first_giver.
With the first giver identified, we start looping through the remaining names. We pull the next name, and assign that name to receiver. This allows us to make the first match, of the form (giver, receiver). We check this match, and return False if it fails the call to check_match(). If it passes that check, we append the tuple to matches. Before moving on to the next name, we assign the current receiver to giver, making them the next person to give a gift.4
The loop ends when there are no names left. At that point, the first giver and the final receiver need to be paired up. We check that match, and if it passes we can return the set of matches.
Finding a working set of matches
Now we’re ready to use these functions, and hopefully get a working set of matches.
num_attempts = 0
while num_attempts < 10:
num_attempts += 1
matches = attempt_match(names[:])
if matches:
# Print summary, and exit.
print(num_attempts)
summarize_matches(matches)
sys.exit()
# Failed to find a good match.
print("Couldn't make a good set of matches.")I’m not sure how hard it is to find a working set of matches, so I’m setting a limit of 10 attempts for now. On each pass through the main loop, we call attempt_match(). That function will either return False, or a good set of matches. If we have a good set of matches, we print a summary of the matches and exit. I’m always curious how many attempts it takes, so I’m also printing that number.
If the loop ends without making a good match, we display a clear message to that effect.
Here’s the summarize_matches() function:
def summarize_matches(matches):
for giver, receiver in matches:
print(f"{giver} will give to {receiver}.")This works:
5
Jasmine will give to Joshua.
Joshua will give to Alexandra.
Alexandra will give to Joel.
Joel will give to Jeremiah.
Jeremiah will give to Eric.
Eric will give to Catherine.
Catherine will give to Sherri.
Sherri will give to Terri.In this run, it took 5 attempts to find a good set of matches. Running the program a few times, I saw it generate a good set of matches in 1 attempt, and I saw it take up to 7 attempts.
Sharing with family
As soon as this worked, I copied the output text and sent it to our family’s group text. I was quite intentional about sending the very first set of matches that met our family’s constraints. I’ll admit a little temptation to look over the matches, and see if I think they’re “good”. But that feels pretty bad, and even for a small thing like a gift exchange you really want to keep the trust your family has in you to be impartial.
A bit of lightness…
There’s a great joke to be had here, and I wonder if anyone reading has been thinking of it. I rewrote the function summarize_matches() slightly:
def summarize_matches(matches):
for giver, receiver in matches:
print(f"{giver} will give to Eric.")This generates some very agreeable output:
Jeremiah will give to Eric.
Jasmine will give to Eric.
Sherri will give to Eric.
Catherine will give to Eric.
Terri will give to Eric.
Alexandra will give to Eric.
Joel will give to Eric.I wrote a message to the family group text saying there was an issue with the initial output, and pasted this in as the corrected output. My immediate family groaned and sent facepalm emojis, but I quickly got more appropriately amused responses from my extended family.
Improvements
Before reading about other implementations, I found a significantly better approach just by writing this post. A lot of times I find that a bit of writing lets me see things more clearly. Sometimes that comes from writing a post, sometimes it’s writing to a colleague, and sometimes it comes from writing documentation.
As I was writing out the explanation for attempt_match(), I realized I could work directly with list indexes, rather than using intermediate variables such as giver and receiver. This version requires much less code:
def attempt_match(names):
random.shuffle(names)
# Match each person with the next, then match the last
# person with the first.
matches = [(names[i], names[i+1]) for i in range(len(names)-1)]
matches.append((names[-1], names[0]))
# Check all matches.
if all([check_match(match) for match in matches]):
return matches
return FalseWhat we’re really doing in the earlier approach, after shuffling names, is matching each item in names with the item that follows. That is, we’re matching names[i] with names[i+1]. This doesn’t work for the last name in the list; we instead match that name with the first name in the list.
The code above uses a comprehension to do most of this. This approach lets us make all the matches in just two lines of code.5
With the whole set of matches made, we can use another comprehension to check all the matches in one line of code. Consider this comprehension:
[check_match(match) for match in matches]This calls check_match() for every match in the list matches. It generates a list of boolean values, one for each match in the set of matches that were just generated. The all() function returns True if all values in the list are True. If they are, we return the list matches. If any of these are False, there’s a bad match and we return False to indicate a failed attempt at making an acceptable set of matches.
Conclusions
This was an interesting little exercise. I was going to do a bit more reading about mathematically elegant solutions to this problem, but the final version of attempt_match() is clean enough to satisfy my curiosity about this kind of problem for now.
If I were writing a version of this program to serve a high-traffic site, I’d take the time to read up on mathematically efficient models of this kind of problem. For example if I were implementing the matching algorithm for a game lobby, I’d want to use the most efficient approach.
Have you written any fun little programs to make your family life a little better? If so, please share your story! :)
Resources
You can find the code files from this post in the mostly_python GitHub repository.
If you haven’t used Faker before, it’s great for generating small and large amounts of sample data. After running pip install faker, here’s the code for generating this list of names:
>>> from faker import Faker
>>> fake = Faker()
>>> names = [fake.first_name() for _ in range(9)]
>>> names
['Sherri', 'Peter', 'Terri', ..., 'Jeremiah']This list was generated using the default en_US locale; you can generate names from a wide range of locales. You can also generate much more than just names. See the documentation for more.
Note that reversed(match) returns an iterator, not a tuple:
>>> match = ('Sherri', 'Eric')
>>> rev_match = reversed(match)
>>> rev_match
<reversed object at 0x104655bd0>
>>> tuple(rev_match)
('Eric', 'Sherri')Wrapping the iterator in a call to tuple() returns a tuple that we can use in our comparisons.
Writing this sentence was the moment when I realized there was a much simpler way to implement this! But this is also why I like working with Python; you can reason things out, develop solutions that make sense, and then develop more concise solutions. You don’t have to come up with an elegant solution right away.
Revisiting this code again after publication, I realized the bold line here is not used:
def attempt_match(names):
...
while names:
...
# Current receiver becomes next giver.
giver = receiver
# The last receiver gives to the first giver.
match = (receiver, first_giver)
if not check_match(match):
return False
# If we're still here, all matches are good.
return matchesOriginally I used the following code every time I defined a match:
match = (giver, receiver)In order to use this exact code, I had to assign the right names to giver and receiver. I later realized I could just make the final match using the final value of receiver, and first_giver.
I’m leaving the incorrect code in the post, because one of the main points here is that exploratory code is often messy, including lines that aren’t actually needed. The final version of the program does not use these lines.
If it’s hard to make sense of the comprehension as written, see if the multiline version is more clear:
matches = [
(names[i], names[i + 1])
for i in range(len(names) - 1)
]
matches.append((names[-1], names[0]))The first line of the expression generates a tuple of the form (giver, receiver). The second line generates the index values to loop over. We want to use the indices from 0 through one less than the length of the list. For more about comprehensions, see MP #5.
Also, on my final review of this post, I realized you can make all the matches inside the comprehension:
matches = [
(names[i], names[i + 1])
for i in range(-1, len(names) - 1)
]By starting the range at -1, the first iteration of the loop in the comprehension matches the last person with the first person.

