Python Lists: A closer look, part 4

MP #8: When are tuples a better choice than lists?

Note: The previous post in this series discussed the list comprehensions. The next post discusses how to profile Python programs, so you’ll be able to measure the impact of any optimizations you make in your code.

Tuples are often introduced as "lists that don't change". This is a reasonable first way to think about tuples, but there are more nuanced ways of understanding tuples. For example tuples use memory more efficiently than lists, and that can have a significant impact on how efficiently your program runs.

Lists are so useful that it can be tempting to use them whenever you need to work with a sequence. If they're working for the problem you're trying to solve, and the performance of your program is adequate, then there's no pressing need to use a different data structure. But there are a number of other sequences you can use, that fit specific situations. In this installment we'll look at when it's appropriate to use tuples, and how the choice to use a tuple can affect the performance characteristics of your programs.

What is a tuple?

A tuple is an immutable sequence; we'll get to that word in more detail in a moment. It's helpful first to consider the kinds of things you can do with a tuple, and what you can't do. You can do any of the following with a tuple:

• Get an element from the tuple.

• Loop over the tuple, or loop over part of the tuple.

• Check if an item is in the tuple, or not in the tuple.

There are some things you can't do with a tuple:

• Add an element to the tuple.

• Replace an element.

• Remove an element.

What does “immutable” mean?

Tuples are often described as "immutable", without much discussion about what that means beyond "they can't be changed". Whether an object is mutable or immutable has a significant impact on how the language handles that object. Immutable objects are easier for a language to manage, because once the object is stored in memory it may be accessed multiple times, but it can never be added to or modified in any way.

This distinction becomes slightly more complicated to think about when you consider variables. A variable is a reference to a value. We can change the value that a variable refers to, which makes it a little harder to think about immutability. Keep in mind it's the value that's immutable and can't be changed; you can change what a variable refers to any time you want.

To see this more clearly, lets write a program that stores the first five prime numbers in a list, and then prints the list. Then we’ll add another prime to the list, and print the list again:

# primes_list.py

primes = [2, 3, 5, 7, 11]
print(primes)

primes.append(13)
print(primes)

Here's the output:

[2, 3, 5, 7, 11]
[2, 3, 5, 7, 11, 13]

We can do something interesting with this code to understand the concept of mutability better. The id()function accepts any object, and returns a unique identifier that remains the same for the life of the program’s execution. Keep in mind this is the id of the object that the variable refers to; the variable itself doesn't have an id.

If we print the id of the list before and after the call to append(), you'll see that the variable primes points to the same object each time:

primes = [2, 3, 5, 7, 11]
primes_id = id(primes)
print(primes_id, primes)

primes.append(13)
primes_id = id(primes)
print(primes_id, primes)

Here's the output:

4352302144 [2, 3, 5, 7, 11]
4352302144 [2, 3, 5, 7, 11, 13]

Even though the list has changed, it's still the same object in memory. If we try the same thing with a tuple, you'll see that the id changes:

# primes_tuple.py

primes = (2, 3, 5, 7, 11)
primes_id = id(primes)
print(primes_id, primes)

primes = (2, 3, 5, 7, 11, 13)
primes_id = id(primes)
print(primes_id, primes)

Here's the output:

4400460672 (2, 3, 5, 7, 11)
4401240608 (2, 3, 5, 7, 11, 13)

We've changed the value that the variable primes refers to, but we've also created an entirely new object, with a different identifier. This is at the heart of mutability: a mutable object can change in memory; an immutable object can only be replaced by an entirely new object.

All of this has important consequences for how efficiently a program runs.

Making short tuples

Making short tuples often looks like this:

>>> primes = (2, 3, 5, 7, 11)

We can verify that this is a tuple using the type() function:

>>> primes = (2, 3, 5, 7, 11)
>>> type(primes)
<class 'tuple'>

Many people come away from this thinking that parentheses always define tuples, just as square brackets always define lists. That is not accurate. Take a look at this example:

>>> primes = 2, 3, 5, 7, 11
>>> type(primes)
<class 'tuple'>

It's actually the commas that define a tuple. This can throw people off if you need to make a tuple with a single element. Wrapping a single item in parentheses, without a comma, does not create a tuple:

>>> prime = (23)
>>> type(prime)
<class 'int'>

You need to include a comma in order to make a tuple with one item:

>>> prime = (23, )
>>> type(prime)
<class 'tuple'>

You don't need the parentheses, either:

>>> prime = 23,
>>> type(prime)
<class 'tuple'>

These details don't come into play too often. But if you're not aware of this aspect of tuples it can be really hard to debug programs when this is the cause of an error.

Making long tuples

This also matters when you make longer tuples using generator expressions. This looks like it might be a tuple, but it's not:

>>> squares = (x**2 for x in range(1_000_000))
>>> type(squares)
<class 'generator'>

This is a generator expression, as we discussed in the previous post in this series. If you want to work with a long tuple, wrap the generator expression in a call to tuple():

>>> squares = tuple(x**2 for x in range(1_000_000))
>>> type(squares)
<class 'tuple'>

Poker hands

To see the difference using tuples can make, let's look at a real-world example. In the following code, the function get_hand() returns a poker hand. To keep things simple, we'll just look at the values of the cards, and ignore the suits. We'll also write this program using only lists initially, without any significant optimization:

# poker_hands.py

from random import choice

all_cards = [2, 3, 4, 5, 6, 7, 8, 9, 10, 'j', 'q', 'k', 'a']

def get_hand(hand_size=5):
    """Return a hand of cards."""
    return [choice(all_cards) for _ in range(hand_size)]

num_hands = 10
hands = [get_hand() for _ in range(num_hands)]

print(f"\nGenerated {len(hands):,} hands.")
print(hands[0])

We use the choice() function to pull a random card from the list all_cards. In get_hand(), we use a comprehension to return a list of 5 cards; if you want a different hand size, you can pass the number of cards you want to get_hand().

The list hands is generated by another comprehension. In this comprehension, we call get_hand() repeatedly to generate a sequence of poker hands.

At the end of the script we print the number of hands generated. We also print the first hand in the list, so we can make sure it looks like a poker hand. Here's the output:

Generated 10 hands.
[3, 8, 4, 'a', 'a']

So far, so good. Now let's look for a certain kind of hand. In poker, an ace-high straight is a sequence of cards containing a 10, Jack, King, Queen, and Ace.¹ Let's check if the list hands contains any of these straights:

# poker_hands_check_ace_high.py

from random import choice

all_cards = [2, 3, 4, 5, 6, 7, 8, 9, 10, 'j', 'q', 'k', 'a']

def get_hand(hand_size=5):
    """Return a hand of cards."""
    return [choice(all_cards) for _ in range(hand_size)]

def check_ace_high_straight(hand):
    """Check if hand is an ace-high straight."""
    for card in [10, 'j', 'q', 'k', 'a']:
        if card not in hand:
            return False
    return True

num_hands = 5_000_000
hands = [get_hand() for _ in range(num_hands)]

print(f"\nGenerated {len(hands):,} hands.")
print(hands[0])

# Check for any ace-high straights.
winners = []
for hand in hands:
    if check_ace_high_straight(hand):
        winners.append(hand)

if winners:
    print(f"\nFound {len(winners)} winning hands.")
    print(winners[0])
else:
    print("\nNo winning hands found.")

We have a new function called check_ace_high_straight(), that makes sure all of the necessary cards are in the hand for an ace-high straight. If any of these cards is not in the hand, the function returns False. If none of them are missing, the function returns True.

Then we go through the entire list hands, checking each one to see if it meets these conditions. If it does, we add it to the list winners. If there are some winners, we report the number of winning hands and show one of them to verify that things are working correctly.

With only ten hands, you probably won't see any winners. But when I run this against 5,000,000 hands, there are over a thousand winning hands:

Generated 5,000,000 hands.
[7, 8, 7, 'j', 9]

Found 1668 winning hands.
[10, 'k', 'a', 'j', 'q']

This works well, and if it runs fast enough for the number of hands you need to deal with, you might not care to optimize your code at all. But on my system, it takes almost 16 seconds to analyze this many hands. Also, there's something nice about using a wider variety of a language's features once you're familiar with them. Let's look at how tuples can simplify this program.

Where can we use tuples?

There are five lists in this program:

• The list all_cards, which we pull from randomly to make new hands;

• Each hand returned by get_hand() is a list;

• In check_ace_high_straight(), there’s a list of cards that make up the straight;

• hands, which contains all the hands we're working with;

• winners, containing all hands with an ace-high straight.

Let's go through each of these, one at a time. We'll consider not just whether we can use a tuple without generating errors, but whether it will make sense to do so in the context of building a program that deals with poker.

Note: The next post in this series will cover profiling. Profiling tools and strategies allow you to do much more targeted optimization, but going through each possible place to use a tuple in this example will be interesting as well.

The list all_cards

The list all_cards is always used the same way; we just pull cards from it randomly. We never add anything to it, and we never remove anything from it. All we ever do is read from this list.

If you're working on a program like this that simulates hands, it's safe and reasonable to convert this to a tuple. One of the main reasons to keep using a list here is if you're simulating a deck, and you want to remove a card from the list each time it's dealt into a hand.

We're not doing that, so let's replace this with a tuple and see if it breaks the program. If it still works, we'll see if there's any impact on the efficiency of the program:

all_cards = (2, 3, 4, 5, 6, 7, 8, 9, 10, 'j', 'q', 'k', 'a')

We just changed one line. The program still works, but it still takes 15.9 seconds on my system.

The sequence all_cards is created once, but read from many times. The dynamic nature of the list does not impact this program’s performance much, so replacing it with a tuple doesn’t improve the program’s efficiency.

Each hand as a tuple

In this example, every hand is stable as soon as it's drawn. We never remove cards from a hand, and we never add cards to the hand. That's not true for all variations of poker. If your program needs to handle variations of poker with dynamic hands, tuples would not work.

Let's return each hand as a tuple, and see what happens. This only requires a modification to get_hand():

def get_hand(hand_size=5):
    """Return a hand of cards."""
    return tuple(choice(all_cards) for _ in range(hand_size))

Making this one change decreases the program's execution time to 12.6 seconds on my system, for a speedup of just over 20%. That's great!

Changing all_cards() to a tuple didn't help. That data structure was read a bunch of times, but it was only ever created once. In this case, we're changing 5,000,000 data structures from lists to tuples, and then every one of those is read from multiple times when checking for winners. This has a much more significant impact on the overall efficiency of the program.

Note: If you forget to wrap the expression (choice(all_cards) for _ in range(hand_size)) in a call to tuple(), you'll return a generator expression instead. This will be a much slower program (26s on my system), because you're storing all of those generator expressions and then evaluating them multiple times. This is a great example of actual sequences such as lists and tuples being more efficient than generator expressions.

The function check_ace_high_straight()

Here’s the function check_ace_high_straight(), using a tuple instead of a list for the cards we’re looking for:

def check_ace_high_straight(hand):
    """Check if hand is an ace-high straight."""
    for card in (10, 'j', 'q', 'k', 'a'):
        if card not in hand:
            return False
    return True

This has no significant impact on the efficiency of the program. This code is more efficient; if you write a program that creates this tuple 5 million times, it will run about 0.2s faster than a program that creates the same list 5 million times.² But 0.2s is not very significant when the program is taking over 10 seconds to run overall.

The sequence hands

Here’s the sequence hands, defined as a tuple instead of a list:

hands = tuple(get_hand(hand_size=5) for _ in range(num_hands))

Using a tuple here instead of a list makes the program slower by about half a second. List comprehensions are very efficient in Python. The reason for the slowdown here is fairly complicated, but you can think of it as Python having to dynamically generate a sequence, and then turn it into a static tuple.

Making a tuple from a generator expression is slower than making a list from a comprehension. The efficiency of using a tuple after it’s created doesn’t always make up for the time lost in building the tuple in the first place.

The sequence winners

The sequence winners is currently defined in a loop. To make a tuple here, we first need to build winners from a comprehension:

winners = [hand for hand in hands if check_royal_straight(hand)]

Making this change saves about 0.2 seconds. We can check if using a tuple here will change anything:

winners = tuple(hand for hand in hands if check_royal_straight(hand))

This doesn’t significantly change the overall performance of the program.

Before drawing some conclusions, let’s look at the memory characteristics of using tuples.

A tuple as a shelf

In earlier discussions, we used a shelf as a metaphor for a sequence. Here's what that shelf would look like for a tuple:

Since Python knows that a tuple will never change, it creates a shelf that has exactly enough space for the items it references. There's no extra space needed, because nothing will ever be added to it.

Memory footprint of tuples

If we examine the memory footprint of a tuple, we'll find that a tuple is always smaller than a list with the same number of items in it. This is true for the smallest sequences:

>>> squares_tuple = (1,)
>>> sys.getsizeof(squares_tuple)
48
>>> squares_list = [1]
>>> sys.getsizeof(squares_list)
64

And this is true for longer sequences as well:

>>> squares_tuple = tuple(x**2 for x in range(1_000_000))
>>> sys.getsizeof(squares_tuple)
8000040
>>> squares_list = [x**2 for x in range(1_000_000)]
>>> sys.getsizeof(squares_list)
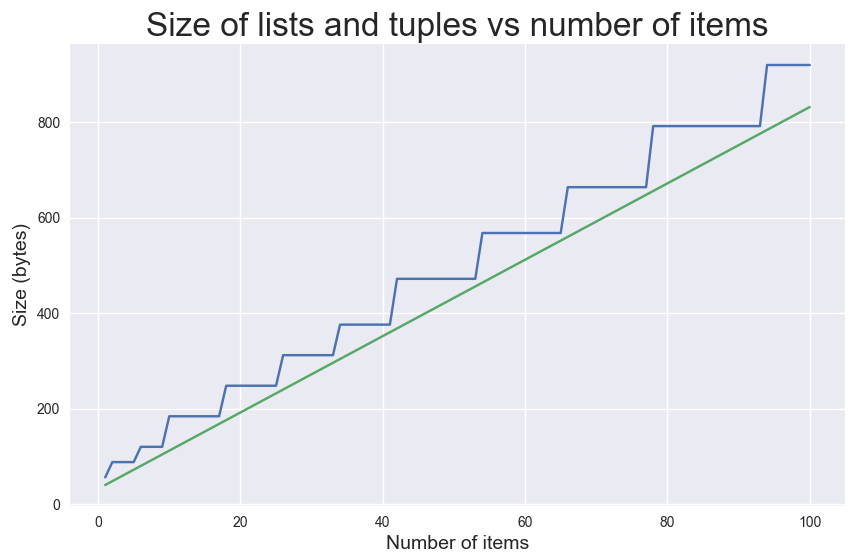
8448728

It's interesting to compare the size of a tuple to the size of a list, across a wide range of sequence lengths:

The size of a tuple increases linearly; there is no stepped shape, because additional space is never allocated for a tuple. Lists always keep a little extra space to accomodate new elements, so they always take up more space in memory than a tuple of the same length. (The code that generates this plot is left as an exercise, but the solution is available if you just want to see the code.)

Conclusions

When you're creating a sequence, consider whether it will need to be modified over the life of the program. If it won't, consider using a tuple where you've been using lists, especially if the choice of which one to use impacts your program's performance significantly.

In the next post, we'll look at how to profile Python code. This will help us get away from simply timing how long it takes to run a program, which depends on how busy your system is overall. Profiling will keep us from having to guess which parts of our code to optimize, and show us exactly which parts of a program are taking longer than others. It will also allow precise testing of different optimization strategies.

Resources

You can find the code files from this post in the mostly_python GitHub repository.

Further exploration

1. Generate a plot showing that tuples always take up less space in memory than lists with the same number of elements. If you get stuck or want to compare your solution to mine, you can see the code I used here.

2. In poker_hands.py, the body of check_ace_high_straight() can be written in one line using the all() function. Try rewriting the function using all(); you can see the solution here.

3. Extend the poker_hands.py example to include card suits as well as card values.

1. A royal flush, or royal straight flush, is an ace-high straight where all of the cards are in the same suit. We’re not considering suits in this example, so we’ll just look for ace-high straights.

2. To verify this, run straight_cards_list.py and then straight_cards_tuple.py from the programs for this post. The tuple-based version should run faster than the list-based version.